Ми навчилися диференціювати прості алгебраїчні функції, такі як \(x^2 + c\) або \(ax^4\), і тепер маємо розібратись, як диференціювати суму двох або більше функцій.
Наприклад, нехай \[ y = (x^2+c) + (ax^4+b); \] тоді яким буде \(\dfrac{dy}{dx}\)? Як ми будемо працювати над цією задачею?
Відповідь на це запитання досить проста: продиференціюйте їх одну за одною таким чином: \[ \dfrac{dy}{dx} = 2x + 4ax^3. \]
Якщо у вас є сумніви, чи це правильно, спробуйте більш загальний випадок, керуючись початковими принципами. І це буде наступний шлях: нехай \[y = u+v,\] де \(u\) — будь-яка функція від \(x\), і \(v\) — будь-яка інша функція від \(x\). Тоді, якщо \(x\) збільшиться до \(x+dx\), \(y\) збільшиться до \(y+dy\); \(u\) збільшиться до \(u+du\); і \(v\) до \(v+dv\). І матимемо: \(y+dy = u+du + v+dv.\) Віднімаючи початкове \(y = u+v\), отримуємо \(dy = du+dv,\) і поділивши це на \(dx\), отримаємо: \[\dfrac{dy}{dx} = \dfrac{du}{dx} + \dfrac{dv}{dx}.\]
Це відповідає описаній вище процедурі. Ви диференціюєте кожну функцію окремо та складаєте результати. Отже, якщо тепер ми візьмемо наведений у попередньому параграфі приклад та введемо значення двох функцій, ми матимемо, використовуючи нотацію наведену у розділі III, \[\begin{alignat*}{2} \frac{dy}{dx} & = \frac{d(x^2+c)}{dx} &&+ \frac{d(ax^4+b)} {dx} \\ & = 2x &&+ 4ax^3, \end{alignat*}\] так само, як і раніше.
Якби було три функції від \(x\), які ми можемо назвати \(u\), \(v\) і \(w\), так що \[\begin{align*} y &= u+v+w; \\ \text{тоді}\; \frac{dy}{dx} &= \frac{du}{dx} + \frac{dv}{dx} + \frac{dw}{dx}. \end{align*}\]
З цього одразу випливає правило для віднімання, адже якби функція \(v\) сама була від’ємною, її диференціальний коефіцієнт також був би від’ємним; так що диференціюючи \[\begin{align*} y &= uv, \\ \text{ ми маємо отримати}\; \frac{dy}{dx} &= \frac{du}{dx} - \frac{dv}{dx}. \end{align*}\]
Але коли ми маємо справу з добутком, стає трохи складніше.
Припустімо, що нас попросили продиференціювати вираз \[ y = (x^2+c) × (ax^4+b), \] що нам робити? Результатом точно не буде \(2x × 4ax^3\); оскільки легко побачити, що ані \(c × ax^4\), ані \(x^2 × b\) не було б взято до цього добутку.
Тепер є два шляхи, якими ми можемо приступити до роботи.
Перший спосіб. Виконайте спочатку множення, і потім, розв’язавши його, диференціюйте.
Відповідно, ми множимо \(x^2 + c\) на \(ax^4 + b\).
Це дає \(ax^6 + acx^4 + bx^2 + bc\).
Тепер диференціюємо та отримаємо: \[ \dfrac{dy}{dx} = 6ax^5 + 4acx^3 + 2bx. \]
Другий спосіб. Повернемося до початкових принципів і розглянемо рівняння \[ y = u × v; \] де \(u\) — одна функція від \(x\), а \(v\) — будь-яка інша функція від \(x\). Тоді, якщо \(x\) зростає до \(x+dx\); і \(y\) до \(y+dy\); і \(u\) стає \(u+du\), а \(v\) стає \(v+dv\), ми матимемо: \[\begin{align*} y + dy &= (u + du) × (v + dv) \\ &= u · v + u · dv + v · du + du · dv. \end{align*}\]
Тут \(du · dv\) є малою величиною другого порядку малості, і тому може бути відкинуто, залишивши \[ y + dy = u · v + u · dv + v · du. \]
Тоді, віднявши початкове \(y = u· v\), ми залишимо \[ dy = u · dv + v · du; \] і, поділивши на \(dx\), отримаємо результат: \[ \dfrac{dy}{dx} = u\, \dfrac{dv}{dx} + v\, \dfrac{du}{dx} . \]
Тобто, наші інструкції будуть наступними: Щоб диференціювати добуток двох функцій, помножте кожну функцію на похідну іншої та складіть два отримані таким чином добутки.
Зауважте, що цей процес полягає у наступному: вважайте \(u\) константою під час диференціювання \(v\); потім розглядайте \(v\) як константу, поки ви диференціюєте \(u\); і повна похідна \(\dfrac{dy}{dx}\) буде сумою цих двох результатів.
Тепер, винайшовши це правило, застосуємо його до конкретного прикладу, який розглядався вище.
Ми хочемо продиференціювати добуток \[ (x^2 + c) × (ax^4 + b). \]
Назвемо \((x^2 + c) = u\) та \((ax^4 + b) = v\).
Тоді, за щойно встановленим загальним правилом, ми можемо написати:
точно так само, як і раніше.
Нарешті, ми маємо диференціювати частки.
Розглянемо такий приклад: \(y = \dfrac{bx^5 + c}{x^2 + a}\). У цьому випадку марно намагатися опрацювати ділення заздалегідь, тому що \(x^2 + a\) не ділиться на \(bx^5 + c\), і вони не мають спільного множника. Тож не залишається нічого іншого, як повернутися до початкових принципів і винайти правило. Тому ми візьмемо \[y = \frac{u}{v};\] де \(u\) і \(v\) дві різні функції незалежної змінної \(x\). Тоді, коли \(x\) стане \(x + dx\), \(y\) стане \(y + dy\); і \(u\) стане \(u + du\), а \(v\) стане \(v + dv\). Тоді \[ y + dy = \dfrac{u + du}{v + dv}. \]
Тепер виконаємо алгебраїчне ділення наступним чином: 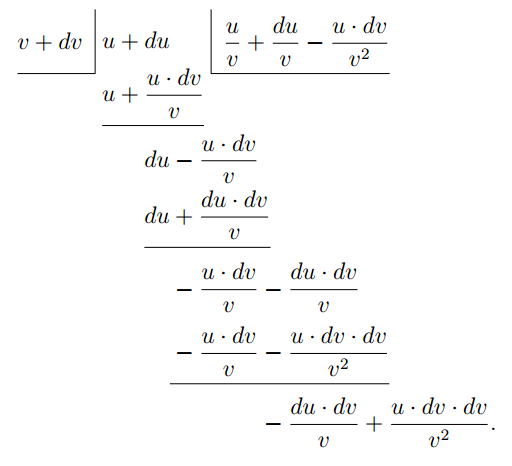
Оскільки обидва ці залишки є малими величинами другого порядку, ними можна знехтувати, і ділення може зупинитися на цьому, оскільки будь-які подальші залишки будуть ще меншими.
Отже, ми отримали: \[\begin{align*} y + dy &= \dfrac{u}{v} + \dfrac{du}{v} - \dfrac{u· dv}{v^2}; \\ \end{align*}\] що може бути записано як \[\begin{align*} &= \dfrac{u}{v} + \dfrac{v· du - u· dv}{v^2}. \\ \end{align*}\] Тепер віднімемо початкове \(y = \dfrac{u}{v}\), і у нас залишиться: \[\begin{align*} dy &= \dfrac{v· du - u· dv}{v^2}; \\ \text{звідки}\; \dfrac{dy}{dx} &= \dfrac{v\, \dfrac{du}{dx} - u\, \dfrac{dv}{dx}}{v^2}. \end{align*}\]
Це дає нам інструкції щодо того, як диференціювати ділення двох функцій. Помножте функцію дільника на похідну функції діленого; потім помножте функцію діленого на похідну функції дільника, і відніміть. Нарешті, поділіть на квадрат функції дільника.
Повертаючись до нашого прикладу \(y = \dfrac{bx^5 + c}{x^2 + a}\), \[\begin{align*} \text{ запишемо}\; bx^5 + c &= u; \\ \text{та}\; x^2 + a &= v. \end{align*}\]
Тоді
Розрахунок часток часто втомлює, але в ньому немає нічого складного.
Далі наведено кілька ще повністю розрахованих прикладів.
(1) Продиференціювати \(y = \dfrac{a}{b^2} x^3 - \dfrac{a^2}{b} x + \dfrac{a^2}{b^2}\).
Будучи константою, \(\dfrac{a^2}{b^2}\) стає нулем, і ми маємо \[ \frac{dy}{dx} = \frac{a}{b^2} × 3 × x^{3-1} - \frac{a^2}{b} × 1 × x^{1-1}. \]
Але \(x^{1-1} = x^0 = 1\); тож ми отримуємо: \[ \frac{dy}{dx} = \frac{3a}{b^2} x^2 - \frac{a^2}{b}. \]
(2) Продиференціюйте \(y = 2a\sqrt{bx^3} - \dfrac{3b \sqrt[3]{a}}{x} - 2\sqrt{ab}\).
Переписавши \(x\) у формі степеня, ми маємо \[ y = 2a\sqrt{b} x^{\frac{3}{2}} - 3b \sqrt[3]{a} x^{-1} - 2\sqrt{ab}. \]
Тепер \[\begin{align*}\frac{dy}{dx} = 2a\sqrt{b} × \tfrac{3}{2} × x^{\frac{3}{2}-1} - 3b\sqrt[3]{a} × (-1) × x^{-1-1}; \\ \text{або, }\; \frac{dy}{dx} = 3a\sqrt{bx} + \frac{3b\sqrt[3]{a}}{x^2}.\end{align*}\]
(3) Продиференціюйте \(z = 1.8 \sqrt[3]{\dfrac{1}{\theta^2}} - \dfrac{4.4}{\sqrt[5]{\theta}} - 27°\).
Це можна записати: \(z= 1.8\, \theta^{-\frac{2}{3}} - 4.4\, \theta^{-\frac{1}{5}} - 27°\).
\(27°\) зникає, і ми маємо \[\begin{align*}\frac{dz}{d\theta} = 1.8 × -\tfrac{2}{3} × \theta^{-\frac{2}{3}-1} - 4.4 × \left(-\tfrac{1}{5}\right)\theta^{-\frac{1}{5}-1}; \\ \text{або}\;, \frac{dz}{d\theta} = -1.2\, \theta^{-\frac{5}{3}} + 0.88\, \theta^{-\frac {6}{5}}; \\ \text{або,}\; \frac{dz}{d\theta} = \frac{0.88}{\sqrt[5]{\theta^6}} - \frac{1.2}{\sqrt[3]{\theta^5}}.\end{align*}\]
(4) Продиференціюйте \(v = (3t^2 - 1.2 t + 1)^3\).
Прямий спосіб зробити це буде пояснено пізніше (див. тут); але ми можемо впоратися з цим зараз без будь-яких труднощів.
Розгортаючи куб, отримуємо
(5) Продиференціюйте \(y = (2x - 3)(x + 1)^2\).
або, простіше кажучи, помножити, а потім продиференціювати.
(6) Продиференціюйте \(y = 0.5 x^3(x-3)\). \[\begin{align*} \frac{dy}{dx} &= 0.5\left[x^3 \frac{d(x-3)}{dx} + (x-3) \frac{d(x^3)}{dx}\right] \\ &= 0.5\left[x^3 + (x-3) × 3x^2\right] = 2x^3 - 4.5x^2. \end{align*}\]
Так само, як і у попередньому прикладі.
(7) Продиференціюйте \(w = \left(\theta + \dfrac{1}{\theta}\right) \left(\sqrt{\theta} + \dfrac{1}{\sqrt{\theta}}\right)\).
Це можна записати як
Це, знову ж таки, можна отримати простіше, спочатку помноживши два множники, а потім продиференціювавши. Однак це не завжди можливо; див., наприклад, тут, приклад 8, в якому правило диференціювання добутку має бути використаним.
(8) Продиференціюйте \(y =\dfrac{a}{1 + a\sqrt{x} + a^2x}\). \[\begin{align*} \frac{dy}{dx} &= \frac{(1 + ax^{\frac{1}{2}} + a^2x) × 0 - a\dfrac{d(1 + ax^{\frac{1}{2}} + a^2x)}{dx}} {(1 + a\sqrt{x} + a^2x)^2} \\ &= - \frac{a(\frac{1}{2}ax^{-\frac{1}{2}} + a^2)} {(1 + ax^{\frac{1}{2}} + a^2x)^2}. \end{align*}\]
(9) Продиференціюйте \(y = \dfrac{x^2}{x^2 + 1}\). \[ \dfrac{dy}{dx} = \dfrac{(x^2 + 1)\, 2x - x^2 × 2x}{(x^2 + 1)^2} = \dfrac{2x}{(x^2 + 1)^2}. \]
(10) Продиференціюйте \(y = \dfrac{a + \sqrt{x}}{a - \sqrt{x}}\).
У формі степеня, \(y = \dfrac{a + x^{\frac{1}{2}}}{a - x^{\frac{1}{2}}}\).
(11) Продиференціювати
\[\begin{align*} \theta &= \frac{1 - a \sqrt[3]{t^2}}{1 + a \sqrt[2]{t^3}}. \\ \text{Тепер}\; \theta &= \frac{1 - at^{\frac{2}{3}}}{1 + at^{\frac{3}{2}}}. \end{align*}\] \[\begin{align*} \frac{d\theta}{dt} &= \frac{(1 + at^{\frac{3}{2}}) (-\tfrac{2}{3} at^{-\frac{1}{3}}) - (1 - at^{\frac{2}{3}}) × \tfrac{3}{2} at^{\frac{1}{2}}} {(1 + at^{\frac{3}{2}})^2} \\ &= \frac{5a^2 \sqrt[6]{t^7} - \dfrac{4a}{\sqrt[3]{t}} - 9a \sqrt[2]{t}} {6(1 + a \sqrt[2]{t^3})^2}. \end{align*}\]
(12) Резервуар квадратного поперечного перерізу має сторони, нахилені до вертикалі під кутом \(45°\). Сторона дна становить \(200\) футів. Знайдіть вираз для кількості води, яка вливається або витікає, коли глибина води змінюється на \(1\) фут; отже, знайдіть у галонах кількість, що вилучається щогодини, коли глибина зменшується з \(14\) до \(10\) футів за \(24\) години.
Об’єм усіченої піраміди висотою \(H\) і основами \(A\) та \(a\) дорівнює \(V = \dfrac{H}{3} (A + a + \sqrt{Aa} )\). Легко побачити, що якщо нахил становить \(45°\), а глибина \(h\), довжина сторони квадратної поверхні води становить \(200 + 2h\) футів, отже об’єм води \[\begin{align*}\dfrac{h}{3} [200^2 + (200 + 2h)^2 + 200(200 + 2h)] =\\= 40 000h + 400h^2 + \dfrac{4h^3}{3}.\end{align*}\]
\(\dfrac{dV}{dh} = 40 000 + 800h + 4h^2 = {}\) кубічних футів на фут варіації глибини. Середній рівень від \(14\) до \(10\) футів становить \(12\) футів, коли \(h = 12\), \(\dfrac{dV}{dh} = 50 176\) кубічних футів.
Галони на годину відповідають зміні глибини на \(4\) фути. за \(24\) години \({} = \dfrac{4 × 50 176 × 6.25}{24} = 52 267\) галонів.
(13) Абсолютний тиск, в атмосферах, \(P\), насиченого пару при температурі \(t°\) C. визначено Дюлонгом як \(P = \left( \dfrac{40 + t}{140} \right )^5\), доки \(t\) вище \(80°\). Знайти швидкість зміни тиску з температурою при 100°С.
Розкладемо чисельник за біноміальною теоремою (див. тут).\[\begin{align*}P = \frac{1}{140^5} (40^5 + 5×40^4 t + 10 × 40^3 t^2 +\\+ 10 × 40^2 t^3 + 5 × 40t^4 + t^5); \end{align*}\]
якщо \(t = 100\), це становить \(0.036\) атмосфери на зміну температури на один градус Цельсія.
(1) Диференціюйте
(a) \(u = 1 + x + \dfrac{x^2}{1 × 2} + \dfrac{x^3}{1 × 2 × 3} + \dotsb\).
(b) \(y = ax^2 + bx + c\). (c ) \(y = (x + a)^2\).
(d) \(y = (x + a)^3\).
(2) Якщо \(w = at - \frac{1}{2}bt^2\), знайдіть \(\dfrac{dw}{dt}\).
(3) Знайдіть похідну \[ y = (x + \sqrt{-1}) × (x - \sqrt{-1}). \]
(4) Продиференціюйте \[ y = (197x - 34x^2) × (7 + 22x - 83x^3). \]
(5) Якщо \(x = (y + 3) × (y + 5)\), знайдіть \(\dfrac{dx}{dy}\).
(6) Продиференціюйте \(y = 1.3709x × (112.6 + 45.202x^2)\).
Знайдіть похідні від
(7) \(y = \dfrac{2x + 3}{3x + 2}\).
(8) \(y = \dfrac{1 + x + 2x^2 + 3x^3}{1 + x + 2x^2}\).
(9) \(y = \dfrac{ax + b}{cx + d}\).
(10) \(y = \dfrac{x^n + a}{x^{-n} + b}\).
(11) Температура \(t\) нитки електричної лампи розжарювання пов'язана зі струмом, що проходить через лампу, співвідношенням \[ C = a + bt + ct^2. \]
Знайдіть вираз, що відповідає зміні сили струму при зміні температури.
(12) Наступні формули були запропоновані для вираження співвідношення між електричним опором \(R\) дроту при температурі \(t°\) C. та опором \(R_0\) цього самого дроту при \(0°\) за Цельсієм, \(a\), \(b\), \(c\) є константами. \[\begin{align*} R &= R_0(1 + at + bt^2). \\ R &= R_0(1 + at + b\sqrt{t}). \\ R &= R_0(1 + at + bt^2)^{-1}. \end{align*}\]
Знайдіть швидкість зміни опору залежно від температури, що визначається кожною з цих формул.
(13) Виявлено, що електрорушійна сила \(E\) певного типу гальванічного елемента змінюється залежно від температури \(t\) відповідно до співвідношення
\[\begin{align*}E = 1.4340 \bigl[1 - 0.000814(t-15)+ \\+ 0.000007 (t-15)^2\bigr] \text{ вольт}.\end{align*}\]
Знайдіть зміну електрорушійної сили на градус при \(15°\), \(20°\) і \(25°\).
(14) Електрорушійна сила, необхідна для підтримки електричної дуги довжиною \(l\) зі струмом інтенсивності \(i\), була встановлена місис Айртон, як \[ E = a + bl + \frac{c + kl} {i}, \] де \(a\), \(b\), \(c\), \(k\) константи.
Знайдіть вираз для зміни електрорушійної сили (a) з урахуванням довжини дуги; (b) з урахуванням сили струму.
(1) (a) \(1 + x + \dfrac{x^2}{2} + \dfrac{x^3}{6} + \dfrac{x^4}{24} + \ldots\)
(b) \(2ax + b\).
(c ) \(2x + 2a\).
(d) \(3x^2 + 6ax + 3a^2\).
(2) \(\dfrac{dw}{dt} = a - bt\).
(3) \(\dfrac{dy}{dx} = 2x\).
(4)
(5) \(\dfrac{dx}{dy} = 2y + 8\).
(6) \(185.9022654x^2 + 154.36334\).
(7) \(\dfrac{-5}{(3x + 2)^2}\).
(8) \(\dfrac{6x^4 + 6x^3 + 9x^2}{(1 + x + 2x^2)^2}\).
(9) \(\dfrac{ad - bc}{(cx + d)^2}\).
(10) \(\dfrac{anx^{-n-1} + bnx^{n-1} + 2nx^{-1}}{(x^{-n} + b)^2}\).
(11) \(b + 2ct\).
(12) \(R_0(a + 2bt)\), \(R_0 \left(a + \dfrac{b}{2\sqrt{t}}\right)\), \(-\dfrac{R_0(a + 2bt)}{(1 + at + bt^2)^2}\) or \(\dfrac{R^2 (a + 2bt)}{R_0}\).
(13) \(1.4340(0.000014t - 0.001024)\), \(-0.00117\), \(-0.00107\),
\(-0.00097\).
(14) \(\dfrac{dE}{dl} = b + \dfrac{k}{i}\), \(\dfrac{dE}{di} = -\dfrac{c + kl}{i^2}\).